L’analyse du centre de gravité d’un oscillateur est essentielle pour comprendre son comportement dans divers systèmes physiques. Ce concept repose sur la capacité d’un système à osciller de manière régulière, et sa compréhension permet de déterminer les paramètres fondamentaux qui influencent ces oscillations. En s’intéressant à un oscillateur harmonique, par exemple, on peut observer comment les forces en présence, telles que la pesanteur et la réaction normale, interagissent pour équilibrer le mouvement du système. De plus, l’étude du comportement des oscillateurs mécaniques ouvre la voie à une exploration approfondie des phénomènes de mouvement liés à des conditions initiales spécifiques, renforçant ainsi notre compréhension des mécanismes oscillatoires qui régissent la dynamique des systèmes.
L’analyse du centre de gravité dans le contexte des oscillateurs est essentielle pour comprendre le comportement dynamique d’un système oscillant. En examinant le centre de gravité, nous pouvons déterminer comment la masse est répartie et comment cette distribution influence les oscillations. Dans cet article, nous allons explorer les avantages et les inconvénients de cette analyse, afin de mettre en lumière son importance et ses limitations.
Avantages
L’un des principaux avantages de l’analyse du centre de gravité d’un oscillateur est la simplification qu’elle apporte à la compréhension du mouvement. En concentrant toute la masse du système à un point unique, il devient plus facile d’appliquer les principes de la mécanique pour prédire le comportement dynamique. Cette approche est particulièrement utile lors de l’étude des oscillateurs harmoniques, où le mouvement est régulier et prévisible.
Un autre bénéfice réside dans la possibilité de modéliser les trajectoires de phase lors de l’analyse des oscillations. En fixant la position du centre de gravité, on peut observer comment les forces agissent sur le système au fil du temps. Cela permet d’étudier des systèmes à un degré de liberté avec une efficacité accrue, rendant l’analyse plus intuitive et visuelle. De plus, savoir localiser le centre de gravité aide à mieux concevoir des oscillateurs, que ce soit en termes de performance ou de sécurité.
Analyse approfondie de l’indicateur TRIX en trading
Dans le monde du trading, il est essentiel de disposer d’outils efficaces pour analyser les mouvements du marché. L’un de ces outils est l’indicateur TRIX, qui repose sur une moyenne mobile triple exponentielle. Cet indicateur permet de fournir aux traders…
Inconvénients
De plus, la modélisation basée sur le centre de gravité suppose que la masse est uniformément répartie, ce qui est rarement le cas dans des systèmes pratiques. Cette simplification peut conduire à des erreurs de prédiction significatives, surtout lorsque les conditions externes ou internes changent de manière imprévisible. En conséquence, bien qu’utilisée couramment, l’analyse du centre de gravité doit être complétée par d’autres méthodes pour une évaluation complète des oscillateurs.
L’analyse du centre de gravité d’un oscillateur permet de comprendre comment les forces en présence influent sur le mouvement d’un système oscillant. Cela revêt une importance cruciale, tant dans les applications mécaniques que dans l’analyse technique dans le domaine financier. Grâce à des principes tels que ceux des oscillateurs harmoniques, nous pouvons déduire des comportements dynamiques qui vont bien au-delà des simples oscillations, en tenant compte des aspects tels que les oscillations libres et les influences externes.
Analyse du momentum à long terme avec l’indicateur Schaff
L’analyse du momentum à long terme constitue un élément clé dans le domaine du trading et de l’investissement. L’indicateur Schaff se distingue par sa capacité à mesurer la force des tendances du marché, offrant ainsi aux traders des outils efficaces…
Oscillateurs mécaniques et leur fonctionnement
Les oscillateurs mécaniques sont des systèmes capables de afficher une variation périodique de leur position. Lorsqu’une masse, fixée par un ressort par exemple, est mise en mouvement, elle effectue des oscillations autour de sa position d’équilibre. Le centre de gravité G de ce système joue un rôle central dans ce mouvement, car il est le point où toute la masse peut être considérée comme concentrée. Ce concept s’avère essentiel dans l’étude des oscillations harmonies, où le mouvement est décrit par des fonctions périodiques.
Régression linéaire : un outil puissant pour l’analyse technique
La régression linéaire s’impose comme un outil puissant pour l’analyse technique, transformant la manière dont les investisseurs abordent le marché boursier. En offrant une représentation claire des tendances pratiques, cet outil mathématique permet d’identifier les relations entre les prix des…
Importance du centre de gravité dans les oscillations
Dans le cadre du mouvement d’un oscillateur, la condition d’équilibre P + R = 0, où P est la force de pesanteur et R la réaction normale, doit être étudiée de près. L’analyse du centre de gravité permet de visualiser comment ces forces se compensent et influent sur l’équilibre du système. Cela est particulièrement pertinent pour des oscillateurs à un degré de liberté, où les équations différentielles qui décrivent le comportement du système peuvent être simplifiées grâce à des observations sur le centre de gravité.
DiNapoli et les stochastiques préférés : une approche technique
L’approche technique dans le domaine du trading est essentielle pour analyser et prédire les mouvements des marchés. Parmi les outils développés, le Stochastique DiNapoli se distingue comme un oscillateur performant, conçu par le célèbre trader Joe DiNapoli. Fort de plus…
Trajectoires de phase et conditions initiales
L’une des approches pour étudier le comportement d’un oscillateur consiste à analyser les portraits de phase. En observant une trajectoire à partir d’un point représentatif des conditions initiales, on peut comprendre comment le système évolue au fil du temps. Cet outil est inclu dans la méthodologie d’analyse technique, permettant d’identifier des tendances sur des périodes données, ceci d’autant plus pertinent pour quiconque s’intéresse à l’évolution des marchés financiers.
Moyenne mobile modifiée : une approche innovante en analyse technique
L’utilisation des moyennes mobiles en analyse technique joue un rôle essentiel dans l’interprétation des mouvements des prix sur les marchés financiers. Parmi les variantes de cet outil, la moyenne mobile modifiée, ou Modified Moving Average (MMA), se démarque par son…
Application dans l’analyse technique des tendances des devises
Dans le monde du trading, comprendre le comportement des oscillateurs permet d’optimiser les stratégies d’investissement. La notion de centre de gravité est tout aussi pertinente ici, car elle peut aider à identifier des points d’inversion ou des moments de consolidation. En intégrant ces concepts au sein de l’analyse technique, les traders peuvent mieux appréhender les fluctuations des devises et potentiellement anticiper les mouvements futurs. Pour approfondir cette approche, vous pouvez consulter un transfert de connaissances savantes ici : Analyse technique des tendances des devises.
L’analyse du centre de gravité d’un oscillateur est fondamentale pour comprendre son comportement dynamique. Cela permet de déceler les forces en présence et d’anticiper les mouvements de l’oscillateur, qu’il soit mécanique ou électronique. En effet, comprendre les oscillations peut s’avérer crucial dans des domaines tels que la mécanique, l’électronique ou même dans l’analyse technique des marchés financiers.
Comprendre les canaux de Keltner en analyse technique
Les canaux de Keltner représentent un outil essentiel en analyse technique pour les traders souhaitant évaluer les fluctuations et la tendance des prix d’un actif. Cet indicateur, qui s’appuie sur la volatilité du marché, se distingue par sa structure en…
Compréhension du concept de centre de gravité
Le centre de gravité d’un système est défini comme le point où la masse totale du système peut être considérée comme concentrée. En d’autres termes, c’est le point d’application de la résultante des forces agissant sur le système. Pour un oscillateur, il est essentiel de déterminer ce point, car cela influence directement son équilibre et son comportement dynamique.
L’analyse technique des tendances des devises
L’analyse technique des tendances des devises est un outil indispensable pour tout trader cherchant à naviguer efficacement dans le marché des changes. En se basant sur l’observation des mouvements passés des prix et des volumes, cette méthode permet d’identifier des…
Application à l’oscillateur harmonique
Dans le cas d’un oscillateur harmonique, la mise en mouvement du système repose sur l’équilibre entre la force de gravité et la force de ressort. En écartant une masse attachée à un ressort et en la relâchant, on peut observer une oscillation symétrique autour du centre de gravité. Ce mouvement oscillatoire permet d’explorer les caractéristiques intrinsèques du système comme la fréquence et la période.
Formation analyse technique en trading : les clés pour réussir
La formation en analyse technique constitue un élément essentiel pour tout trader souhaitant réussir sur les marchés financiers. Elle permet de comprendre les *bases* de cette technique d’analyse, qui repose sur l’étude des graphiques et des indicateurs techniques. À travers…
Rôle des forces en présence
Il est important de prendre en compte les différentes forces agissant sur l’oscillateur. La force de pesanteur et la réaction normale doivent s’équilibrer pour maintenir le système en mouvement. Une analyse approfondie des forces permet de mieux appréhender le comportement oscillatoire. Une identification précise de ces forces aide également à la modélisation mathématique de l’oscillateur à l’aide d’équations différentielles.
Utilisation des outils numériques pour l’analyse
De nos jours, des outils numériques sont disponibles pour faciliter l’analyse du centre de gravité d’un oscillateur. L’utilisation d’ordinateurs et de logiciels dédiés permet de visualiser les mouvements du centre de gravité en temps réel et d’effectuer des simulations précises. Ces outils sont particulièrement utiles pour établir des graphiques de trajectoires de phase et pour modéliser des systèmes oscillants complexes.
Importance de la modélisation dans l’analyse technique
Enfin, dans le cadre de l’analyse technique des marchés financiers, le concept du centre de gravité des oscillateurs prend tout son sens. Les indicateurs oscillateurs sont fréquemment utilisés pour évaluer les tendances des devises et anticiper les mouvements de prix. Comprendre la dynamique du centre de gravité d’un oscillateur peut donc contribuer à améliorer les stratégies de trading et la prise de décisions sur les marchés.
L’analyse du centre de gravité d’un oscillateur est essentielle pour comprendre son comportement. Elle permet d’examiner comment une masse se déplace et oscille autour d’un point d’équilibre. Cette analyse est particulièrement utile dans les sciences physiques et l’ingénierie, où la compréhension de ces mouvements peut éclairer des applications pratiques, allant des structures mécaniques aux appareils électroniques.
Avantage
Un des principaux avantages de l’analyse du centre de gravité de l’oscillateur est sa capacité à simplifier le modèle physique d’un système complexe. En représentant le système comme un point matériel concentrant toute la masse, on peut facilement appliquer des lois de la dynamique pour prévoir son comportement. Cela est particulièrement pertinent dans le cas des oscillateurs harmoniques, où les mouvements périodiques peuvent être prévisibles et répétitifs.
De plus, cette analyse facilite la mesure des paramètres dynamiques, comme la fréquence angulaire et la période d’oscillation. En étudiant le centre de gravité, on peut mieux comprendre les forces d’équilibre en jeu, telles que la force de pesanteur et la réaction normale. Cela entraîne une meilleure conception de systèmes mécaniques, notamment pour améliorer la stabilité des structures qui subissent des vibrations.
Inconvénients
En outre, l’analyse du centre de gravité néglige parfois les non-linéarités qui peuvent exister dans des systèmes complexes. Lorsque les oscillations dépassent un certain seuil, les modèles linéaires deviennent insuffisants pour décrire le comportement réel de l’oscillateur. Cela peut mener à des erreurs dans les prévisions et les calculs, rendant essentielle une approche plus complète qui intègre les effets anharmoniques.
Dans cette analyse, nous allons explorer le concept du centre de gravité dans le cadre d’un oscillateur. En effet, la compréhension du centre de gravité est cruciale pour appréhender le mouvement d’un oscillateur harmonique. Nous verrons comment il influencie la dynamique de l’oscillation et comment il peut être mesuré à travers des paramètres physiques spécifiques.
Définition du centre de gravité
Le centre de gravité est le point dans un système où la masse totale peut être considérée comme étant concentrée. Dans le cas d’un oscillateur, il est important de comprendre que ce point influencera non seulement la stabilité du système, mais aussi la manière dont il oscillera. Lorsque le centre de gravité est bien localisé, cela permet d’assurer un équilibre optimal, favorisant un mouvement harmonieux.
Oscillation et effets de la gravité
Dans un oscillateur, la force de pesanteur agit directement sur une masse suspendue. Cette force doit être équilibrée par la réaction normale pour établir un mouvement stable et régulier. En écartant la masse d’un point d’équilibre, il est possible d’étudier comment la force de gravité et l’oscillation interagissent. Ainsi, l’analyse du centre de gravité devient essentielle pour déterminer l’angle et la vitesse associés à l’oscillation.
Configuration d’un oscillateur harmonique
Lorsque l’on considère un oscillateur harmonique, par exemple un ressort, il est nécessaire de ramener la masse à son centre d’inertie. Ce dernier est le point où se concentre la masse et il définit les propriétés du mouvement de l’oscillateur. La position exacte du centre de gravité peut impacter la fréquence et l’amplitude des oscillations, ce qui constitue un aspect fondamental de l’analyse dynamique.
Trajectoires de phase et oscillations
Un élément clé dans l’étude des oscillations est le portrait de phase, qui montre la relation entre la position et la vitesse d’un système oscillant. Cette représentation permet de visualiser comment le centre de gravité évolue au cours du temps. En enregistrant la position de ce point à l’aide d’outils numériques, les chercheurs peuvent déterminer la stabilité et la prévisibilité des mouvements oscillatoires.
Application pratique de l’analyse du centre de gravité
Dans le domaine de l’analyse technique, la connaissance du centre de gravité d’un oscillateur peut être appliquée pour prévoir des mouvements de marché. Par exemple, en utilisant des oscillateurs en finance, on peut analyser les tendances et établir des stratégies d’investissement. Comprendre la dynamique du centre de gravité peut ainsi fournir des indicateurs sur les variations des prix de manière très précise.
Dans cet article, nous allons explorer l’analyse du centre de gravité d’un oscillateur. Comprendre comment le centre de gravité influence le comportement oscillatoire d’un système est essentiel pour déchiffrer les dynamiques des oscillateurs. Nous aborderons divers concepts tels que la définition du centre de gravité, son rôle dans l’oscillation, et les implications pratiques de cette analyse.
Qu’est-ce que le centre de gravité ?
Le centre de gravité d’un objet est le point où la masse totale peut être considérée comme étant concentrée. Dans le cadre des oscillateurs, il est crucial car il détermine la stabilité et le mouvement du système. Lorsque la masse est uniformément distribuée, le centre de gravité se trouve au centre de l’objet, mais des distributions inégales peuvent le déplacer vers des zones particulières, affectant ainsi le comportement dynamique.
Influence du centre de gravité sur l’oscillation
Le centre de gravité d’un système oscillant détermine la manière dont les forces, telles que la force de gravité et les forces de réaction, interagissent lors de l’oscillation. Une position idéale du centre de gravité assure un équilibre entre ces forces, permettant aux oscillations de se produire sans interférence. Si le centre de gravité est mal positionné, cela peut entraîner des mouvements chaotiques et des déséquilibres, rendant l’oscillateur moins efficace.
Étude dynamique du centre de gravité
Pour analyser le comportement d’un oscillateur, il est nécessaire de modéliser les forces agissant sur le centre de gravité. Les équations différentielles sont souvent utilisées pour décrire la dynamique de ces systèmes. Par exemple, la méthode d’analyse dynamique peut permettre de prédire à quel moment et comment le centre de gravité se déplacera, influençant ainsi les oscillations du système.
Applications pratiques de l’analyse
Les connaissances sur le centre de gravité dans les oscillateurs peuvent être appliquées dans divers domaines, y compris l’ingénierie, la robotique et même l’animation. Une compréhension approfondie permet aux ingénieurs de concevoir des systèmes plus stables et plus performants, tout en minimisant les risques de défaillance dus à une mauvaise gestion du centre de gravité.
En somme, l’analyse du centre de gravité d’un oscillateur est un aspect fondamental dans la compréhension des systèmes dynamiques. En maîtrisant ces concepts, il est possible d’améliorer la performance et la stabilité des dispositifs oscillants, tout en appliquant cette connaissance dans des contextes variés.
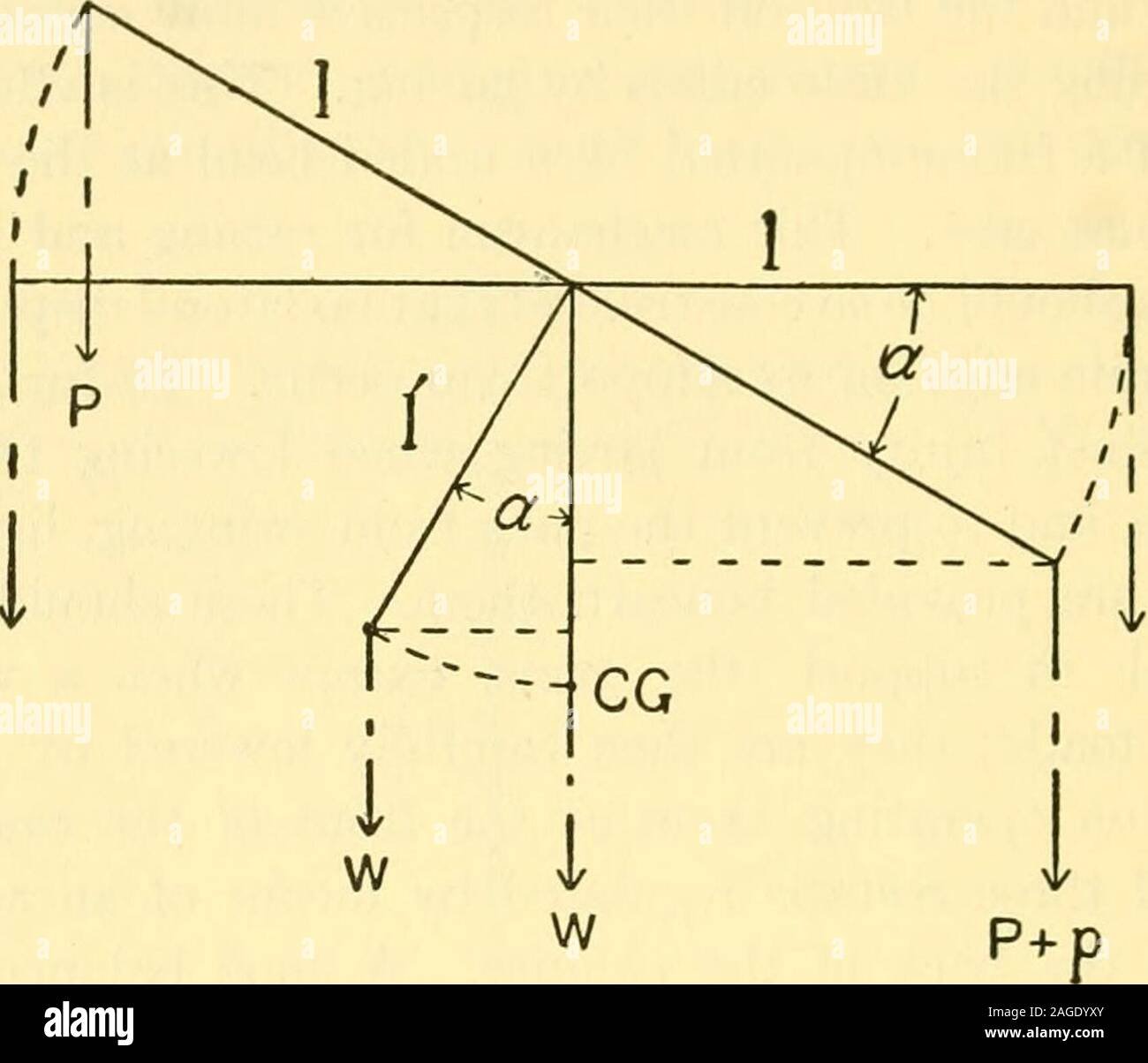
| Paramètre | Description |
| Centre de gravité | Point où la masse est concentrée, influençant la stabilité. |
| Force de pesanteur | Agit sur le centre de gravité, provoquant des oscillations. |
| Réaction normale | Force opposée à la pesanteur, maintient l’équilibre. |
| Mouvement harmonique | Résultat de l’interaction entre pesanteur et réaction. |
| Équations différentielles | Modélisent le comportement dynamique de l’oscillateur. |
| Amplitude | Distance maximale à partir de l’équilibre, déterminée par l’énergie. |
| Période | Temps nécessaire pour accomplir un cycle complet d’oscillation. |
| Un degré de liberté | Système pouvant osciller dans une seule direction. |
Témoignages sur l’Analyse du Centre de Gravité de l’Oscillateur
Lors de mes premières expériences avec les oscillateurs mécaniques, j’ai été particulièrement fasciné par l’idée que le mouvement du centre de gravité d’un système pouvait être modélisé comme celui d’un point unique où toute la masse est concentrée. Cela simplifie énormément l’analyse, car cela permet de considérer les effets de la gravité et de la réaction normale sur le mouvement de l’ensemble avec une approche beaucoup plus claire.
Un étudiant a partagé son expérience sur l’étude des oscillateurs harmoniques. D’après lui, comprendre que l’équilibre entre la force de pesanteur et la réaction normale est essentiel pour donner un sens au mouvement des oscillateurs a été une révélation. « Une fois que j’ai réalisé que ces forces s’équilibrent pour définir la condition d’oscillation, » explique-t-il, « j’ai pu visualiser le comportement de la masse suspendue et son interaction avec le ressort. » Cela lui a permis d’appréhender plus facilement la notion d’oscillation libre.
Un autre témoignage d’un formateur mentionne l’importance d’utiliser des outils numériques pour suivre et analyser les trajectoires des oscillateurs. Par exemple, il raconte comment l’enregistrement du mouvement du centre de gravité à l’aide d’un ordinateur a révolutionné sa façon d’enseigner. Cet outil lui a permis de dresser des graphes précis des portraits de phase et d’observer les comportements non-linéaires, offrant à ses élèves une perspective enrichissante sur les systèmes oscillants.
La modélisation des systèmes oscillants à un degré de liberté s’est également avérée être un excellent moyen d’intégrer les équations différentielles au sein de l’apprentissage. Un participant à nos cours a témoigné : « Comprendre que les phénomènes physiques dépendant du temps peuvent être décrits par des équations ajustées dans un cadre de mouvements oscillatoires a véritablement solidifié ma compréhension de la dynamique des systèmes. » Cela a également permis d’établir un lien entre la théorie et la pratique.
Enfin, nombreux sont ceux qui ont constaté l’impact que les indicateurs d’oscillateur peuvent avoir sur leur analyse technique. « En utilisant ces indicateurs pour anticiper les tendances », affirme un analyste, « j’ai pu affiner mes décisions, tant dans le trading que dans l’étude des mouvements physiques dans différents milieux. » Cet aspect met en lumière la pertinence de l’analyse du centre de gravité dans divers domaines, allant bien au-delà de la simple mécanique.
L’analyse du centre de gravité d’un oscillateur est essentielle pour comprendre son comportement dynamique. Ce concept permet de décrire comment un système oscillant, comme un oscillateur harmonique, se déplace et réagit aux forces qui s’exercent sur lui. En étudiant le centre de gravité d’un oscillateur, nous pouvons mieux appréhender les caractéristiques de ses mouvements périodiques et identifier les facteurs influençant ces oscillations.
Concept de centre de gravité
Le centre de gravité d’un système est le point où la masse totale de l’objet peut être considérée comme concentrée. Pour un oscillateur à un degré de liberté, cela signifie que l’ensemble de la masse peut être ramené à une seule position qui détermine les mouvements du système. En général, le théorème du centre de gravité stipule que lorsque cette masse est soumise à des forces extérieures, telles que la force de pesanteur ou des forces de réaction, le mouvement du centre de gravité peut être analysé de manière plus simple. C’est là que réside l’importance de considérer ce point dans l’étude des oscillateurs.
Mouvement des oscillateurs
Un oscillateur harmonique, par exemple, est un modèle qui illustre parfaitement ce type de mouvement. Lorsque l’on écarte la masse attachée à un ressort, celle-ci commence à osciller autour de sa position d’équilibre. Les forces mises en jeu, telles que la réaction normale et la force de pesanteur, s’équilibrent, ce qui permet à l’oscillateur de maintenir un mouvement périodique. La fréquence angulaire de cet oscillateur décrit la rapidité avec laquelle il peut compléter un cycle d’oscillation. Plus cette fréquence est élevée, plus les oscillations se produisent rapidement.
Propriétés des oscillateurs
Un système oscillant est caractérisé par ses propriétés spécifiques. Parmi celles-ci, la dissipation d’énergie, la non-linéarité et les réponses à diverses excitations externes jouent un rôle fondamental. Par exemple, un oscillateur non linéaire peut avoir une dynamique beaucoup plus complexe, où les mouvements ne sont pas nécessairement périodiques. Cela souligne l’importance d’analyser les trajectoires de phase, où l’on peut visualiser l’évolution des états du système à partir d’un point de condition initiale donné.
Mesure et utilisation des oscillateurs
Pour étudier l’oscillateur, on peut utiliser des outils variés, comme des appareils numériques reliés à des tables de digitalisation, qui permettent de tracer la position du centre de gravité au cours du temps. Cette technique est particulièrement utile pour comprendre les comportements des systèmes oscillants et extraire des données pertinentes sur les vibrations. Les résultats obtenus peuvent ensuite être appliqués dans divers domaines, tels que l’analyse technique en finance, où les oscillateurs sont souvent utilisés pour anticiper les mouvements de tendance des valeurs boursières.
Conclusion de l’analyse du centre de gravité
En résumé, l’analyse du centre de gravité des oscillateurs constitue une approche fondamentale pour comprendre les comportements oscillatoires dans divers systèmes physiques. Que ce soit dans le cadre d’un oscillateur harmonique ou d’un système plus complexe, cet outil d’analyse offre des perspectives précieuses sur les mouvements et les interactions des forces en jeu.
Lorsque l’on aborde l’analyse du centre de gravité d’un oscillateur, il est crucial de comprendre que ce point est déterminant pour le comportement du système. En effet, le centre de gravité représente un point où toute la masse d’un système peut être considérée comme concentrée, ce qui facilite l’étude des oscillations et de leurs caractéristiques.
Le mouvement d’un oscillateur est souvent influencé par des forces externes telles que la force de pesanteur et la réaction normale. Cela nous amène à analyser comment ces forces s’équilibrent afin de déterminer le mouvement du centre de gravité. Par exemple, lorsque la masse est écartée de sa position d’équilibre, elle subit une force de rappel qui a tendance à ramener le système vers sa position initiale. C’est là que l’on peut observer un comportement harmonique bien défini, typique des systèmes oscillatoires.
En langage mathématique, le mouvement d’un oscillateur harmonique peut être décrit à travers des équations différentielles, qui prennent en compte les variations périodiques de la position du centre de gravité. Cette approche permet de prédire avec précision le comportement futur de l’oscillateur, ouvrant ainsi la voie à des applications variées dans des domaines tels que la mécanique ou même l’électronique.
Il est également essentiel de considérer les conditions initiales qui influencent l’évolution du système. En effet, chaque trajectoire de phase d’un oscillateur est définie par son état initial, qui peut être analytique ou numérique selon les outils utilisés. L’analyse de ces paramètres est primordiale pour une compréhension approfondie du fonctionnement et des caractéristiques des oscillateurs à un degré de liberté.
FAQ sur l’analyse du centre de gravité de l’oscillateur
Q : Qu’est-ce qu’un oscillateur ? Un oscillateur est un système capable de maintenir une variation périodique pour au moins l’un de ses paramètres au fil du temps.
Q : Quelle est la définition de la fréquence angulaire ω ? La fréquence angulaire ω correspond à la vitesse à laquelle une oscillation complète peut être réalisée.
Q : Comment le mouvement du centre de gravité est-il décrit dans un oscillateur ? Le mouvement du centre de gravité d’un système est représenté comme celui d’un point matériel où l’ensemble de la masse est concentrée.
Q : Qu’est-ce qu’un oscillateur harmonique ? Un oscillateur harmonique décrit le comportement d’un système à un degré de liberté qui évolue autour d’une position d’équilibre.
Q : Quelles forces sont en équilibre dans un oscillateur ? Dans un oscillateur, la force de pesanteur et la réaction normale s’équilibrent, générant une force nette nulle.
Q : Comment détermine-t-on la période d’un oscillateur ? La période d’un oscillateur peut être déterminée à partir des propriétés physiques du système et des équations différentielles qui le régissent.
Q : Quelle est l’importance de l’analyse technique sur les oscillateurs ? L’analyse technique utilise les oscillateurs pour évaluer les tendances des mouvements de prix sur les marchés financiers.
L’analyse du centre de gravité d’un oscillateur est essentielle pour comprendre le fonctionnement et le comportement dynamique de ce système. Le centre de gravité, souvent symbolisé par la lettre G, représente le point où la masse totale d’un corps est concentrée. Dans le cadre d’un oscillateur mécanique, le mouvement de ce centre est fortement lié aux forces qui agissent sur le système.
Un oscillateur harmonique est un système qui présente des oscillations régulières et périodiques. Dans le cas le plus simple, il peut être modélisé par une masse accrochée à un ressort idéal. Lorsque l’on écarte la masse du centre de gravité, il subit une force de rappel, provoquée par le ressort, qui vise à ramener la masse à sa position d’équilibre. C’est cette interaction entre la force de rappel et la gravité qui fournit les bases d’une oscillation stable.
La fréquence angulaire, notée ω, est un paramètre clé dans l’analyse des oscillateurs. Elle détermine la vitesse d’une oscillation complète et est liée à la période de l’oscillation. En effet, plus la fréquence angulaire est élevée, plus le système oscille rapidement. La compréhension de ce concept permet d’anticiper les comportements oscillatoires d’un système en fonction de ses caractéristiques physiques.
Dans un système oscillant à un degré de liberté, comme un pendule simple ou un ressort, les mouvements sont souvent décrits par des équations différentielles. Ces équations permettent d’étudier la position, la vitesse et l’accélération du centre de gravité au cours du temps, fournissant ainsi des informations sur l’évolution du système. De plus, ces analyses permettent de déterminer les conditions d’oscillation, garantissant que la masse revient sans cesse à sa position d’équilibre.
Les oscillateurs peuvent être classés en oscillateurs linéaires et non-linéaires. Les premiers suivent des règles simples et prévisibles, tandis que les seconds présentent des comportements plus complexes. L’importance de cette distinction réside dans le fait que le mouvement du centre de gravité dans un oscillateur non-linéaire peut être imprévisible et chaotique, rendant plus difficile l’analyse et la prévision de ses comportements.
Un autre aspect intéressant de l’analyse du centre de gravité est la possibilité d’explorer des concepts avancés tels que les portraits de phase. Ces graphiques représentent l’état d’un système dynamique à différents moments et permettent de visualiser l’évolution du centre de gravité au fil du temps. Cette approche graphique est particulièrement utile pour identifier les comportements permanents et transitoires dans un système oscillant.
Enfin, l’utilisation d’outils modernes, comme les logiciels de simulation et les ordinateurs, a révolutionné l’analyse des systèmes oscillants. Grâce à ces technologies, il est possible de collecter et d’analyser des données précises sur le mouvement du centre de gravité, facilitant la recherche sur la dynamique des oscillateurs.
En conclusion, l’analyse du centre de gravité d’un oscillateur est un domaine riche et complexe qui requiert une compréhension approfondie des principes physiques sous-jacents. Que ce soit à travers les oscillateurs harmoniques ou en explorant des systèmes plus complexes, la maîtrise de ce concept est cruciale pour les professionnels et les chercheurs désireux d’approfondir leurs connaissances sur les phénomènes oscillatoires.
